GMU Math MakerLab: Level Sets

MATH 493: Math Through 3D Printing

Level Sets

Anneliese Slaton

“"Well, then, if a Point by moving three inches, makes a Line of three inches represented by three; and if a straight Line of three inches, moving parallel to itself, makes a Square of three inches every way, represented by three-to-the-second; it must be that a Square of three inches every way, moving somehow parallel to itself (but I don't see how) must make Something else (but I don't see what) of three inches every way—and this must be represented by three-to-the-third.’”

- Edwin. A. Abbot, Flatland: A Romance of Many Dimensions

The challenge of representing n-dimensional objects (when n > 3) in a 3D space is one that has plagued the work for centuries. Mathematicians have been studying four-dimensional space since the time of Lagrange to present day.

One way to represent 4D space is to utilize level sets, a concept taught in multivariable calculus. Consider a function f(x,y,z). It is impossible to draw this, as it resides in 4D space. So instead, we choose a constant c to set f(x,y,z) equal to - this allows us to work in three dimensions, while observing how the function changes as c varies.

A level set is a real-valued function of the form

L_c(f) = {(x₁, …, x_n) | f(x₁, …, x_n) = c}.

To help us visualize a 4D graph, I printed the level sets of f(x,y,z)=e^xyz with four c values: c = 1, e, e², e³. The level sets were then placed on the same graph. To print, they were connected with a series of supports through the centers of each graph piece.

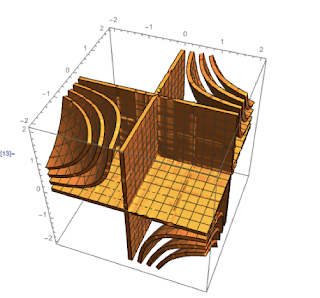Since f is differentiable, the level sets are hypersurfaces and, outside of the critical point of f at (0, 0, 0), they are manifolds (topological spaces that locally resemble Euclidean space). Additionally, because f is differentiable, we know that the gradient of f at some point x is either 0 or perpendicular to the level set at the same point x.

Level sets can be used in the Level Set Method, a method that utilizes level sets for numerical analysis of surfaces and shapes.

The object to be printed was created using Mathematica and OpenScad for the supports. It was printed on the Makerbot 5th Generation

printer.