Fun with Fractals
By Hope Roberts
George Mason University
Math 493
Mathematics through 3D Printing
What are Iterated Functions &
Fractals?
Iterated functions are a way of constructing Fractals.
An iterated function takes a function
X → X and composes another function of itself a
repeated amount of times. (Wikipedia).
Repeating the same function over and over is known as
iteration.
After so many iterations the structure is seen to shrink.
This is known as limiting behavior. The set will converge to a single fixed
point, which is known as the attractive fixed point.
Example of a self-similar repeating pattern.
Fractals are patterns that repeat infinitely. The
patterns repeated are complex and self-similar. The repeated patterns are
created by recursion, so repeating a pattern in a similar way.
Brief
History on Iterated Functions
Iterated functions are credited to John E Hutchinson
discovered in 1981.
Michael Barnsley’s is credited with making them popular
in a book he wrote titled Fractals.
Making of my Fractal
Using OpenSCAD with code given by Dr. Sander I changed the
design of the Fractal by adjusting the set of rules of the fractal, specifically changing r,
s and theta in the code. Changing the r,s and theta of the code by any amount
yielded a different shape.
I obtained these values from a yale.edu (reference at
bottom)
The type picked from this website was (o).
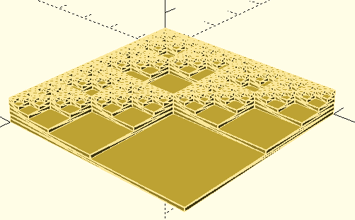
Original structure
before the code was adjusted.
I then adjusted the length and width in the code so that the
platform and bases were supporting the structure in such a way that the
printing would have support in all areas of the structure. Finally I added one
additional layer of height to the structure from 5 levels to 6 levels also increasing
the height of each layer, which increased the thickness of each layer.
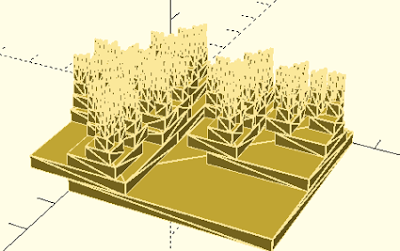
My Fractal after
adjustments to r,s, theta, length, width and height.
In MakerBot I adjusted the size to a four-hour approximate
time for printing, making sure the structure was flat on the surface with
supports and rafts.
Equations & Code Changes:
Below is the
basic equation for an iterated function.
if for all components of f, it is in X
Below are my
values for r, s and theta for my Fractal:
scale1x = -.5; scale2x = .5; scale3x = .5; scale1y = .5; scale2y = .5; scale3y =
.5; theta1 = 90;
theta2 = -90; theta3 = 0;
Below are my
values for the changes to length, width and height in my code.
len = 45; // length of the first segment wid = 45; // width of
the first segment height = 3.0; //
height of the first cube.
Finished Product:
The finished
product was successful and there was relatively no clean up of the structure
involved.
Sources:


No comments:
Post a Comment